Modeling and Evaluation Models Discussion
Foreword: The following write-up is an excerpt from a COVID-19 project aimed to predict death rates caused by COVID-19 virus from publicly available data; thus, effectively answer the question of feasibility of using publicly available data for the prognostics.
The last step in CRISP-DM methodology is the deployment of models for data mining, which emphasizes practical application of models. Industry term for practical application of models is “putting models in production.”
Preparation of models for successful deployment requires understanding of technological and human resources needed for successful deployment of data mining operation. In the context of the COVID-19 analysis – the deployment phase of CRISP-DM methodology requires models to be tailored to the circumstances surrounding Covid-19 pandemic, which are the availability of computational resources, the ease of use of the models for targeted audience – medical practitioners and scientific community, and the over-all practical maintenance of the models once deployed.
Therefore, the following analysis focuses on developing models with increasing complexity: the simpler model with acceptable accuracy – the more practical is the deployment phase.
The analysis deploys models with varying complexity to establish the best trade-off between bias (capturing the pattern in the data) and variance (the range of predictions) on an unseen data.
Important to emphasize is testing a model on the same set of data the model uses for training, produces false sense of accuracy because the model achieves, virtually, perfect fit. In other words, the model replicates prediction target values, y”, from the training prediction target values, y with inconsequential margin of error. The described behavior of a model is known as over-fitting data.
To avoid possible over-fitting, and under-fitting alike, of a model and gauge how well the model predicts outcome when deployed on an unseen datasets, the following analysis utilizes datasets splits in multiple ratios to establish generalization error – an error measuring the outcome of models applied on an unseen test set. Too small of generalization error indicates the model is over-fitting the data, whilst a large generalization error suggests the model is under-fitting the data.
Parametric v. non-parametric models
The algorithms in the analysis are a mix of parametric and non-parametric models. The importance of distinguishing between parametric and non-parametric models in the context of the following analysis – is in complexity of the models: parametric models are far less complex in comparison to non-parametric models. Parametric models have a finite number of parameters, while non-parametric models’ number of parameters grows with number of variables (features) included in the datasets. Thus, the distinction between the two types plays a major role in production run-times where number of features varies significantly between different datasets. Parametric models are computationally faster: they have limited number of parameters to tune and can use smaller datasets to train prior to its deployment in production. The non-parametric models are, generally, more accurate, but the trade-off is they need for large datasets, which translates to longer prediction times. Thus, in a nutshell – the choice between non-parametric and parametric models is a tradeoff between accuracy and production run-times.
Parametric models deployed in the analysis are logistic regressions (LogReg) and Naïve Bayes. Non-parametric models in the analysis are random forest (RF), Classification and Regression Tree (CART), clustering K-Nearest Neighbors (KNN), and ensemble models – namely Adaptive Boost (AdaBoost), Stacking Classification, which utilizes the following base models: LogReg, KNN, and AdaBoost.
Several variants of the algorithms used in the analysis have not converged, thus have no practical utilization in production. Conversely, other models produce directly comparable results and run-times despite varying inputs, predictor variables, or sampling frames. In addition to experimenting with different models, the number and type of input variables for each model were also varied (i.e., exploring models using principal components as inputs compared to models using the original features).
Models
Logistic Regression
LogReg is often the first choice for classification problems because of its ease of implementation and short run-times. The model uses, “linear combination of explanatory variables [16],” to assess possible outcomes of single classification trial as follows:
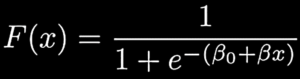
Furthermore, logit function built into the model links F(x) values, “back to a linear combination of the features [16],” in the following manner:

Both logarithmic function functions operate on domain – ∞ to + ∞; thus, LogReg model will accept classification values of any chosen -/+ boundaries, which makes this classification model applicable to wide range of scientific fields, including the following analysis. The loss function of LogReg model is always convex, which is crucial property of the model, because models with convex loss functions are ease to optimize.
LogReg models are susceptible to collinearity and outliers; thus, it is necessary to engineer features to address the consistency of corresponding distributions. The model works well with large datasets and multi-labeled target values; however, on the same token – the size of the datasets may render LogReg ineffective because the model has difficulties capturing complex relationships between multiple variables (features). In other words, as long as the relationships between features are not overly complex – LogReg can handle large datasets. The datasets in the following analysis consists of 17 predictive and one target feature containing binary classes (labels) at the scale of several million records, thus abstruse for LogReg. Moreover, the data assumptions follow linear regression model’s assumptions. Consequently, LogReg model serves as baseline performance, only.
Naïve Bayes
The model’s name is a keepsake of Bayes’ probability theorem, “a formula for calculation probability of an even using prior knowledge of related conditions [16],” defined as follows:
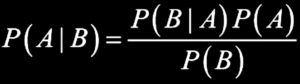
Bayes’ formula estimates probabilities of occurrences, which is a property directly transferable to classification problems by assessing likelihood of certain classes (labels) appearing in a feature. In other words – for classification problems Bayes’ theorem translates to a question: How likely is the label (class) B will occur given the feature value A?
Rewriting the Bayes’ theorem formula to a function, which accounts for relationships between the target variable (y) multiple features (x1 . . . xn), the form changes to the following:
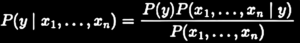
Once we account for the theorem’s,” ‘naïve’ assumption of conditional independence between every pair of features given the value of the class variable [18],” and constant input, the probability formula gets the following form:
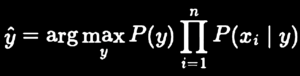
NB model belongs to the family of generative models. As such, NB models can generate new data instances and calculate joint probabilities P(X,y), which suggests they might, under certain conditions and tasks, capture comparatively more information in the data [14].
The model does perform well on classification tasks; however, the probabilities assigned to classes might not be accurate. Moreover, the model has smaller footprint when compared to other models and works well with smaller datasets, especially if independence clause is satisfied in which cases model converges quickly. Alike, the independence clause may cause the model to never converge, dependent classifier’s variant used, as it proves the case in the following analysis where categorical version of NB model (adopted from scikit-learn library) did not converge, whilst its Gaussian variant did. NB models work with binary and multi-label classification problems. NB models are susceptible to size of the datasets and its naiveté about correlation amongst features, oftentimes, does not match the interconnected nature of reality. NB’s performance in this analysis illustrates the listed.
Classification And Regression Tree
Classification and Regression Trees (CART) are simple and easy to understand models. Depending on the output variable, CART models produce either classification (for discrete dependent variables) or regression (for numeric dependent variables) decision trees. CART models are non-parametric and easy to both understand and visualize [21]. According to Trendowicz and Jeffery, “they provide fairly comprehensible predictors in situations where there are many variables which interact in complicated, nonlinear ways [22]”. This is ideal for our data. The model starts with a root node that determines a set of rules creating using the values in the data to predict the dependent variable [21]. These rules then split the data into nodes each with into two distinct branches. This process continues and roots continue to split into different branches until either the model can split no further – this can be because it no longer gains anything from splits, has been through the data exhaustively, or has met a user defined criterion [21]. An example of a user defined stopping criterion is the complexity parameter (cp), which controls whether a node can continue to split. Aside from being easily understandable there are other benefits to the decision trees; decision trees are able to handle a wide range of predictors, require very little preprocessing, perform well with large datasets, and are relatively robust if normal model assumptions are violated [21].
K-Nearest Neighbors
K-Nearest Neighbor model works well in classification and regression tasks. It is a simple lazy-learner algorithm, because it does not perform calculations until it processes an inquiry upon which it provides an answer. The importance of delineating between lazy-learner and an eager-learner has direct consequences on the run-time performance of the model; thus, it is a critical part of the model valuation process.
Eager-learner algorithm estimates (recalculates) various parameters used by the model prior to prediction step, then it re-utilizes the said parameters’ values during the prediction step. Linear regression is an eager-learner: it recalculates parameters a and b of, proverbial, linear function y = ax + b, and reuses them for predictions. Thus, reusing an eager-learner model reuses already estimated (calculated) sets of parameters.
In contrast, reusing a lazy-learner algorithm, such is KNN – the process disregards the previous inquiry and results completely, and restarts as new calculation [15]. This characteristic of lazy-learners makes them quick and less demanding on computing resources during training period, but slow during prediction run-times.
KNN model operates in a metric space, which represents features (Figure 23). Training instances populate metric space and the distances between such instances are the object of measurement. The distances between instances determine the neighborhood and hyper-parameter k specifies number of instances in the neighborhood.
KNN is a non-parametric model: it has no assumptions about the data nor it pre-calculates (estimates) various parameters to for use in prediction phase. Linear regression, as a parametric model, has a list of requirements the data must meet for model’s parameters to work. Because of its non-parametric nature, KNN immediately adopts to changes of input data and delivers predictions. The benefit of KNN’s scalability of input values is obvious in comparison to linear regression model which has to re-estimate given parameters before making new predictions. Nevertheless, linear regression has more efficient run-times due to the pre-calculated parameters.
KNN operates with one-hyper parameter – k and utilizes several distance measurement methods: Euclidean, Manhattan, Minkowski, and Hamming method.
The following analysis uses features with different types of data and different scales amongst same types of data. This renders KNN model ineffective because the model needs homogeneous features: a distance measurement in feature A must translate to the same distance measure in feature B, which is not case with Covid-19 datasets in the following analysis. Alike, KNN is prone to missclassify labels of less common classes found in imbalanced datasets, as it is the case of the datasets used in this research. Both factors, in-homogeneity of the datasets and imbalanced classes in the datasets account for KNN’s poor Recall performance in the following analysis.
Ensemble models
Ensemble methods, as the name suggests, are combinations of different estimators whose collective performance is better than their stand-alone performance. This research utilizes all three ensemble methods: bagging (Random Forest), boosting (Adaptive Boost), and stacking method where KNN, RF, and AdaBoost are comparatively stacked together for performance purpose.
Random Forests
Random forest is a supervised learning algorithm and it uses an ensemble of decision trees to make predictions. RF provides multiple advantages over other models, mainly RF handles large datasets with ease. Another important attribute of RF is it provides an estimate of variables’ importance in the classification problems [9]. Moreover, RF contains two elements of randomness in the algorithm, which is a critical factor for discovery of hidden information in the data. The importance of randomness in the context of the research: the information theory postulates, “the maximum amount of information is carried by the highest uncertainty (unaccredited);” thus, importance of randomness and uncertainty extends beyond philosophical or semantics exercises [13] into practical application by RF model.
The power behind RF model is the use of multiple estimators (trees): each tree uses a random subset of input features to split on, then the algorithm aggregates results produced by individual estimator trees [19].
Two factors drive the design of RF models: the unknown probability distribution of a sample (dataset in analysis), and model’s tendencies overfit the results when used on high-variance data. To aleviate (decrease) possibility of high variance associated unknown probability distribution, RF model attempts to estimate the true distribution of population from samples, and it does it with bagging or bootstrapping technique. Bagging technique draws number of sub-samples from the original sample with replacement then calculating the statistic of the sample. Availability of multiple samples produced by bagging enables the model to calculate statistical uncertainty: Central Limit Theorem suggests, given a trial of N>>1 samples, with true mean X and true standard deviation 𝞼x with sample mean x and sample standard deviation 𝞼[x] ≅ 𝞼x, standard deviation uncertainty range of +/-1 of the true mean of X from the finate sample as follows [11]:
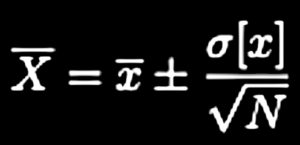
Therefore, bagging method is adequately dubbed a method for estimating uncertainty [12].
For RF model, reducing the uncertainty in the data enables better accuracy by reducing its over-fitting tendencies caused by high variance hidden in samples [12]. In other words: RF is known to provide a high level of accuracy while reducing the risk of over-fitting [10].
RF uses majority voting (sum) to calculate splits in categorical problems, while for regression problems it calculates means. Also, RF is computationally expensive especially as the trees grow.
AdaBoost
Adaptive boost algorithm is known as a weak learner – an estimator marginally better than a random choice. At the core of AdaBoost model is repetitive application of weights to training instances. The assignment of weights modifies training instances creating new values also known as boosting. Adaptive nature of boosting refers to adaptation of weights according to accuracy of predicted instances: instances predicted incorrectly receive increased weights in the next iteration, while the instance predicted correctly received decreased weights. Thus, each sub-sequence iteration of the model over data focuses on instances previously missed. This process continues for certain number of predefined iterations or, theoretically, perfect performance.
In the following analysis, AdaBoost model utilizes Decision Tree (DT) classifier as the base classifier and, inevitably, inherits its strengths and weaknesses. The main strengths of DT classifiers is, the model requires little-to-no data preparation and it can handle numerical and categorical data well. This point is which is critical for the following analysis because Covid-19 datasets is heavy mix of categorical and numerical values. However, the amount of the data affects DT performance: the computational cost of DT is logarithmic as the number of data points increase in the tree. Moreover, slightest variation in data make the model unstable and in case of unbalanced data DT is prone to have some classes dominate. This issue is particularly prevalent in Covid-19 datasets, which affects the accuracy of AdaBoost model. Also, as the complexity of the trees grow, so does over-fitting the data; thus, DT does not generalize data well [17].
Stacking method
Stacking uses meta-estimators to combine prediction of base estimators, which can be any other model. For example, LogReg and NB or NB and AdaBoost models. This analysis deploys this exact combination of models. The principle is stacking model uses training set to train base estimators, then meta-estimator combines base estimators’ predictions and ground truth in more complex ways than voting (sum) or averaging [16].
Discussion to follow.

